Ю.С. Потапов - МНИМОСТЬ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ И ТОРСИОННЫЕ ПОЛЯ

5.1. Энергия и импульс вращательного движения

Итак, мы убедились, что при вращении тела или связанной системы тел их суммарная масса-энергия уменьшается с ростом тангенциальной скорости Vr. согласно релятивистски обобщенной теоремы вириала по закону

(5.1)

имеющему довольно непривычный для СТО вид (здесь).
Но если мы заменим уг на 1/у', то формула (5.1 ) будет иметь вид

(5.2)

похожий на уже привычную нам релятивистскую формулу для полной энергии тела Еп = E0/у. Отметим, что поскольку величина ут принимает значения от 1 до 0, то обратная ей величина у может изменяться в пределах от 1 до бесконечности соответственно.
Построим графики зависимостей ЕЕ от у и Еп от у (см. рис. 5.1). И мы видим математическое чудо: кривая для ЕЕ, представляющая собой полуветвь гиперболы,

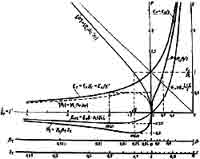Рис. 5.1

простирающуюся влево от оси ординат y =1, плавно и естественно "сшивается" с кривой зависимости Еп от у, простирающейся вправо от оси ординат. Обе кривые составляют одну и ту же ветвь гиперболы!
У графика для Еп, который мы уже строили ранее на рис. 2.1 (а до нас его чертили во многих учебниках СТО,) один конец уходит в бесконечность высоко под потолок (при или при ), а второй раньше обрывался при значении , принимая здесь величину Еп = Е0, и повисал, как стол трамплина, на этой "высоте", принятой нами за единичную. Кривая Еп словно ждала кто бы ее продолжил дальше от этой точки обрыва, столь неестественен был этот обрыв даже с позиций эстетики. Чуть ли не 100 лет ждала. И вот теория движения подсказывает, как продолжить эту оборванную кривую.
Но не слишком ли искусственно мы построили, вернее, даже подстроили это продолжение? Чтобы ответить на такой вопрос, обратим внимание на следующее. Ускорение прямолинейного поступательного движения тела в пространстве ведет к замедлению движения его во времени до значений и к росту полной массы - энергии тела до величин, превышающих его массу-энергию покоя Е0. А ускорение вращения тела ведет к уменьшению его суммарной массы-энергии до величин, меньших Е0. Следовательно, если увязывать полную (или суммарную) массу-энергию тела со скоростью движения его во времени, то естественно сделать вывод, что вращение вроде бы должно вести к ускорению движения тела во времени до величин скорости, больших 1! Значит, безразмерная скорость движения во времени у' которая увеличивается с ростом скорости вращения, для вращающихся тел более естественна, чем скорость уr которая не превышает 1 и уменьшается с ростом скорости вращения.
Кроме того, из уравнения (2.2) следует, что если из приводимой во вращение системы тел "лишняя" масса-энергия уходит только в виде фотонов, у которых скорость движения во времени у = 0, то закон сохранения количества движения во времени требует, чтобы скорость движения самой этой системы во времени возрастала при этом до значений, больших единицы.
Однако если , то из основного уравнения нашей теории движения

(5.3)

следует, что ß'2(в квадрате) - величина отрицательная. А это значит, что отвечающая ей безразмерная тангенциальная скорость мнимая величина. При этом абсолютная величина последней скорости изменяется в пределах .
Но ведь именно такие значения принимали величины ß и у в рассмотренном нами в разделе (1.5) "вертикальном запредельном мире мальтийского икса". Там на оси ординат мы откладывали действительные значения скорости у движения точки во времени при у . А вот скорость ß движения той же точки в пространстве при y > 1 там была мнимой. Получается, что тот таинственный "вертикальный запредельный мир", оказывается, описывает вращательное движение тел?!
Вы спросите: разве можно реальную тангенциальную скорость вращательного движения считать мнимой величиной? Но выше мы уже вроде бы договорились, что при вращательном движении естественнее и удобнее иметь дело с , а не с . Значит, хочешь, не хочешь а надо иметь дело и с мнимой ß'. И действительно, почему бы не считать тангенциальную скорость вращающегося тела мнимой? Ведь при вращении того же диска мы не увидим перемещений его в пространстве, если центр массы диска остается на месте. Более того, если поверхность диска отполирована, то мы не сможем по внешнему виду отличить вращающийся диск от неподвижного. Мы только можем знать (мнить), что один из них вращается. Потому-то мы должны смириться с мыслью о том, что вращательное движение - мнимое.
С другой стороны, ранее в разделе 4.3 мы уже пробовали обобщить движение частицы во времени с внутренним (микроскопическим) вращением материи в ней. Теперь это обобщение мы можем расширить и взглянуть на него с другой стороны: макроскопическое вращение тела - это тоже движение его во времени. Только со скоростью, большей единицы.
Если время на вращающихся телах идет быстрее, чем на неподвижных, то это не так уж сложно обнаружить экспериментально. Тем более, что СТО предсказывала не ускорение, а замедление хода часов, движущихся с высокой тангенциальной скоростью, принимавшейся почти всеми при больших радиусах вращения, мало отличающейся от прямолинейной. И такие эксперименты проводились.
В [37] рассказывается, что еще в начале 60-х годов экспериментаторы обнаружили при измерениях с помощью эффекта Мессбауэра, что центростремительное ускорение вроде бы не замедляет хода часов на быстро вращающихся роторах. (Мы пишем "вроде бы" потому, что точность измерений оказалась все еще недостаточной для твердой уверенности.) На основании принципа эквивалентности Эйнштейна ожидалось, что центростремительное ускорение будет действовать тождественно гравитационному полю, т.е. замедлять ход часов. Не потому ли он не замедлялся, что эффект ускорения хода времени на вращающемся теле, о котором мы предположили в данном разделе, работает в противоположную сторону и компенсирует релятивистское замедление хода времени, вызываемое движением часов с большой тангенциальной скоростью? К сожалению, в указанной публикации результаты экспериментов изложены не очень подробно, чтобы сделать однозначные выводы.
Еще на заре космонавтики предлагались эксперименты по выявлению релятивистского замедления хода времени на искусственных спутниках Земли, летящих, как известно, со скоростью 7,9 км/с [38]. Для этого предлагалось поместить на спутник атомные часы и после длительного пребывания их на орбите сравнить их показания с такими же часами, оставшимися на Земле. Ожидаемое по СТО отставание хода часов на спутнике должно было составлять секунды в год. С помощью атомных часов измерить такую разницу хода времени вроде не составляет большой сложности.
Прошло более 30 лет, а о результатах таких экспериментов пресса что-то не сообщала. Неужели атомные часы до сих пор не побывали в космосе? Ведь чего только туда не запускали за эти годы! Даже атомную бомбу взрывали на орбите спутника Земли. А небольшим атомным часам так и не нашлось места? Думается, что запускали и неоднократно. Только результаты тех экспериментов, наверно, не укладывались в прокрустово ложе СТО. А в эти годы все, что противоречило теории относительности, либо засекречивалось, либо замалчивалось. Это лишь в благословенные времена Майкельсона "отрицательный" результат его эксперимента 1897 г. был немедленно оглашен и обсуждался всей читающей публикой. (И только один А. Эйнштейн до конца своих дней уверял, что он до публикации своей теории в 1905 г. не слышал об опытах Майкельсона.)
А В.М. Мигунов из Запорожья спрашивает: не потому ли и эксперимент Майкельсона дал отрицательный результат, что система отсчета (Земля) в нем была не инерциальной, а двигалась по круговой орбите вокруг Солнца? [39]. Да, вращательное движение уже доставило много неприятностей теории относительности. То ли еще будет!
Если эксперименты с часами на орбитальных космических аппаратах по каким-то причинам все же не обеспечивают требуемой точности, то можно предложить другой эксперимент, который однозначно ответит на вопрос об ускорении или замедлении хода времени при вращении тел. В книге [9] указывалось, что в экспериментах на циклических ускорителях пора переходить от электронных и протонных к мезонным пучкам. Первые же такие эксперименты, для осуществления которых не потребуется основательно переделывать уже существующие ускорители, покажут, замедляется или ускоряется движение во времени мюонов и пионов, летящих по круговой орбите с околосветовой скоростью. В этих экспериментах уже не будет стоять вопрос о прецизионной точности измерений, ибо ожидаемое изменение времени "жизни" частиц составит сотни и тысячи раз и будет выявлено сразу.
Ориентирующийся в современной физике читатель подскажет, что движение мезонов по круговой орбите давно реализовано в мезоатомах, в которых вместо электрона вокруг ядра обращается мюон или пион. Мезоатомы научились синтезировать еще в середине XX века [40]. И коль до сих пор не обратили внимание на изменение времени "жизни" мезонов в таких атомах по сравнению со временем "жизни" свободных мезонов, то значит...
Ничего не значит! Дело в том, что тангенциальная скорость движения мезонов вокруг ядра на устойчивых орбитах в таких атомах, как и скорость электрона в резерфордовско - боровской модели атома, составляет -С/137. При столь низких (по релятивистским меркам) скоростях "фактор Лоренца" у = 0,99997 мало отличается от единицы. Поэтому релятивистское изменение времени "жизни" частиц тут выявить практически невозможно. Увы, мезоатом не дает ответа на наш вопрос. Нужны эксперименты на циклических ускорителях. Вот и еще один ответ на вопрос - зачем было строить эти громадины. Впрочем, для нашего эксперимента пригоден и совсем малюсенький циклотрон из тех, что давно списаны на металлолом.
Московский исследователь-"временщик" В. Чернобров из МАИ в 1993 г. рассказал в популярной статье [41] о созданной им действующей модели "машины времени". Он указывает, что "многочисленные опыты подтвердили взаимосвязь между скоростью вращения тела и ходом времени: около оси вращения часы отстают, на периферии - спешат". Это соответствует нашим предположениям.
Вместе с тем Чернобров отмечает, что аномалии времени у вращающихся тел зависят не только от скорости вращения, но и от массы вращающегося тела, возрастая с ростом массы. И указывает на наличие таких аномалий в районе Жигулей, где Волга 20-километровой петлей обходит эти горы. Создаваемый течением могучей реки огромный момент импульса обуславливает ряд аномальных явлений в Жигулях.
Еще большие моменты импульса создаются морскими течениями в местах их поворота. Не этим ли обусловлены таинственные аномалии в "Бермудском треугольнике" и некоторых других местах Мирового океана?
В нашей теории мы пока не добрались до выяснения зависимости хода времени от массы вращающихся тел и создаваемых ими моментов импульса. Такая зависимость, конечно же, должна существовать. Но мы только в начале пути!
Если суммарную массу mE = EE/C2(с квадрат) вращающейся системы тел умножить на ее тангенциальную скорость Vг, (предположим для простоты, что вращается обруч), то получим выражение для импульса или количества вращательного движения:

(5.4)

В отличие от обычного импульса поступательного движения , в это выражение входит не отношение, а произведение безразмерных скоростей ßr и уг. Это вторая особенность вращательного движения, обусловленная появлением дефекта массы системы и влекущая за собой ряд важных следствий.
На рис. 5.1 построены графики зависимости . Их два, потому что каждому значению уг соответствует два значения . Предположим, что положительному значению соответствует вращение тела в одну сторону, отрицательному - в противоположную. Нам вроде бы представляется возможность выбора знака. Впрочем, выбираем не мы, а Природа. Мы только констатируем ее выбор и пытаемся объяснить его, опираясь на законы физики и математики.
А в математике существует правило, согласно которому "сшиваемые" графики двух функций не должны иметь в точке "сшива" изломов, а должны плавно переходить один в другой. Говорят, что тогда функция "гладкая". Вот и мы на рис. 5.1 выбираем тот из двух возможных графиков функции , который в точке у = 1 плавно и без излома продолжает известный график импульса поступательного движения Р(у), рассматривавшийся нами ранее в разделе 2.4 на рис. 2.1.
В данном случае мы выбираем на рис. 5.1 график Рг, лежащий ниже оси абсцисс, то есть описывающий "отрицательные" значения импульса вращения.
В книге [9] отмечалось, что импульс Рг никогда не принимает положительных значений, что он всегда как бы противоположен по знаку импульсу P поступательного Движения того же тела. Здесь мы должны уточнить, что поскольку скорость ßr - мнимая, го и количество вращательного движeния ßr - тоже мнимая величина.
Отрицательным всегда будет квадрат этой величины. И вообще, если перейти на язык квадратичных функций, сплошь и рядом фигурирующих в теории относительности, то мнимые величины, так смущающие некоторых физиков, здесь исчезнут, и мы будем манипулировать только с действительными (положительными отрицательными) величинами: квадратами энергии, импульса, скорости, расстояний, времени. А из того факта, что в большинстве формул теории относительности фигурируют именно квадраты этих величин, можно сделать далеко идущий вывод, что в природе имеют значение только они, а не первые степени этих величин.
Кривая графика Рг на рис. 5.1 напоминает рисунок пятки босой ноги. Она существенно отличается как от графика импульса поступательного движения Р, примыкающего к ней справа от точки у = 1, так и от графика , построенного на том же рисунке для сравнения и представляющего собой ветвь гиперболы. Последняя описывает начальный импульс тангенциального движения тела на орбите без учета возникающего дефекта массы так, словно движение прямолинейное, а не вращательное. Именно с этим импульсом оперируют механики в практических расчетах движений как маховиков машин, так и искусственных спутников Земли, пренебрегая их дефектом массы, который при столь медленных движениях очень мал. Но разница между ходом кривых Рг и P' при больших скоростях ßr показывает, как сильно могут ошибаться те, кто для упрощения вычислений принимает тангенциальную скорость прямолинейной.
Самой существенной особенностью графика Рr отмеченной в книге [9], является наличие у него экстремума - минимума при V = С/|2(корень квадратный из двух). Это та особая скорость, о которой мы уже говорили в разделе 2.4. Экстремум в виде минимума - это уже не точка перегиба, какие мы отмечали там на графиках импульса и энергий движения, а гораздо серьезнее. Минимум на кривой импульсов означает наличие экстремума на графике зависимости кинетической энергии вращения тела от скорости вращения.
И если этот экстремум является минимумом (а похоже, что в данном случае это так), то мы будем иметь яму на графике зависимости кинетической энергии тела от скорости его вращения.
Кинетическая энергия поступательного движения тела в СТО определяется, как мы уже отмечали, разностью между полной (релятивистской) энергией тела Еп и его энергией покоя Eп, и составляет величину
Если по аналогии с этим определить кинетическую энергию вращения тела, имевшего энергию покоя Е0, а при вращении обладающего энергией ЕЕ, то с учетом формулы (5.1 ) должны записать:

(5.5)

Чтобы исследовать функцию Ект (уr) на экстремум, возьмем производную от Екr по dyr. Она равна значению (1 - 2у) и становится равной нулю при значении уг = 1/2 (или при . Итак, мы нашли еще одну особую скорость. На этот раз для кругового движения.
График зависимости Екг от уr приведенный на рис. 5.1, хорошо сшивается с графиком E (у) лишь в случаях, когда мы примем, что энергия Ект - мнимая величина (а ее квадрат - отрицательная величина ).
О том, что найденный экстремум действительно является минимумом функции Ект (уr говорит и то, что вторая производная по dyr от Ект - отрицательна.
Можно, конечно, удивляться тому, что кинетическая энергия вращения - мнимая величина, хотя тело вращается вполне реально. Но не надо забывать, что та кинетическая энергия, которая сообщается телу во время его раскручивания, уходит из системы вместе с её энергией связи. Поэтому ту кинетическую энергию Екг, которой обладает вращающаяся система, пришедшая в состояние динамического равновесия, вполне можно считать мнимой, как и тангенциальную скорость вращения Vr, не приводящую к смещению (переносу) центра масс системы.
До сих пор физики имели дело только с ямами на графиках потенциальной энергии тела, движущегося в той или иной системе, или на графиках полной энергии системы. Такие ямы называются, как известно, потенциальными ямами. Тело, обладающее кинетической энергией, меньшей глубины потенциальной ямы, обречено навсегда остаться в этой яме, то есть быть пленником системы. А при наличии потерь энергии система со временем стремится прийти к состоянию с энергией, соответствующей энергии дна потенциальной ямы, то есть к минимуму энергии.
Может ли наличие ямы на графике кинетической энергии заставить систему, постепенно теряющую энергию, стремиться к состоянию с этой кинетической энергией?
Ответить помогут наблюдательные данные астрономии. История каждой звезды заканчивается, как известно, ее быстрым сжатием, сбрасыванием в космос лишней массы-энергии (это проявляется как вспышка сверхновой) и уплотнением остатка звезды до маленькой (10-18 км) нейтронной звезды, имеющей ядерную плотность. Нейтронные звезды астрономы обнаруживают по их импульсному радиоизлучению, повторяющемуся с частотой аж до 104(10 в четветртой степени) Гц, что обусловлено быстрым вращением этих объектов. Массу нейтронных звезд, называемых еще пульсарами, определяют весьма точно, когда находят их в тесных двойных звездных системах, которых довольно много в небе. (Звезды, как и люди, предпочитают жить парами.) Эти наблюдения показывают, что гравитационный дефект массы типичной нейтронной звезды составляет 10-15% от ее массы [6].
У большинства нейтронных звезд, как легко высчитать из наблюдательных данных, тангенциальная скорость вращения их твердой поверхности составляет примерно . Нет, не до состояния "черных дыр" коллапсирует большинство звезд в конце своего жизненного пути, а именно до нейтронных звезд, находящихся у дна потенциальной ямы графика энергии вращения Ект. Рисунок, напоминающий пятку ноги, объясняет почему нейтронных звезд так много.
Впрочем, мы не открываем здесь Америку, обнаружив минимум на графике кинетической энергии связанной вращающейся системы тел. Подобный минимум (только на графике потенциальной энергии) давно известен в задаче Кеплера об Удержании планеты, описанной, например, в [42]. Мы лишь немножко видоизменили ту задачу применительно к нашим проблемам.

5.2. Точки над i расставляют треугольники импульсов

В разделе 1.2 мы показали, что Эйнштейн и Минковский исходили из неверных представлений о пространстве-времени, в котором мы живем. В результате они неправильно интерпретировали интервал S как расстояние между точками пространства-времени и вынуждены были придумывать "псевдопифагорову теорему", чтобы как-то свести концы с концами в своих алогичных построениях. Кроме того, они упустили из вида мнимую часть квадрата комплексной длины в пространстве-времени.
Было показано, что правильно точку пространства-времени описывает комплексное число (1.18)

в мнимую часть которого входит не лабораторное время t, a собственное время т движущегося тела. Фигурирующее здесь произведение Сr есть не что иное, как пресловутый интервал Sтеории относительности. И означает он отнюдь не расстояние между точками пространства-времени, а всего лишь проекцию этого расстояния на мнимую ось собственного времени. Благодаря коэффициенту С она выражена в тех же единицах длины (метрах), что и проекции на остальные (пространственные) оси координат. Таким образом, наша комплексная плоскость (1,iСr) - это плоскость расстояний: расстояния в пространстве (l) и расстояния во времени (Сr) до заданной точки Z
А вот Ct - это уже расстояние в пространстве-времени до точки Z. Притом

(5.6)

Эту формулу Пифагора поясняет прямоугольный треугольник на рис. 5.2.
Мы повторили здесь эти простые вещи, излагавшиеся в разделе 1.4 (а ранее - в [9]), потому, что простые вещи почему-то хуже всего доходят до понимания читателя. Увы, движение в науке всегда идет к простому через сложное.
Если взять производную по dt от комплексного числа Z, описывающего по (1.18) точку пространства-времени, и возвести эту производную в квадрат, то получим:

(5.6)

(Точка над буквой означает производную по времени t.)

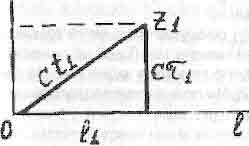Рис. (5.2)

А подставив сюда, будем иметь выражение для квадрат комплексной скорости J движения тела:

(5.8)

Это выражение, представляющее собой новое комплексное число, в котором все члены - квадратичные формы, столь излюбленные теорией относительности, проще получить возведением в квадрат уже известной нам формулы комплексной скорости. Но мы вывели здесь выражение (5.8) более сложным путем затем, чтобы подчеркнуть, что из комплексного числа , характеризующего точку в нашем пространстве-времени, вытекают уравнения, описывающие движение в пространстве-времени.
Этого, увы, не скажешь о комплексном числе , описывающем мировую точку в теории Минковского - Эйнштейна. Потому-то их теория уже в 20-е годы фактически исчерпала себя и не принесла ожидавшихся грандиозных результатов.
В разделе 5.1 мы видели, что мнимая часть 2ßy комплексного числа (5.8) входит сомножителем в выражение (5.4) для количества вращательного движения Рг. Потому-то мы и делаем вывод, что если реальная часть выражения (5.8) для квадрата комплексной скорости J описывает поступательное движение, то мнимая - вращательное, возникающее при поступательном движении тела.
Кроме того, мы делаем очень важный вывод, что вращение является неотъемлемой частью не только любого движения в пространстве, но и неотъемлемым свойством самого пространства-времени. К последнему выводу несложно прийти, вспомнив, что "покой нам только снится", что движение есть неотъемлемое свойство пространства-времени, что если тело неподвижно в пространстве, то уж обязательно движется во времени, и что все тела во Вселенной движутся относительно нее со скоростью , как было показано в [8].
Таким образом, наши предположения о вращательных свойствах пространства и движения в нем, излагавшиеся в разделах 2.5 и 4,3, здесь получают математическое подкрепление.
Но вернемся к треугольникам. В разделе 2.2 мы, домножив почленно основное уравнение (1.16) теории движения

на , получили прямоугольный треугольник импульсов (см. рис. 5.За), описываемый формулой

(5.9)

В нем полный импульс тела Pn = mCполучается как гипотенуза при векторном сложении взаимно перпендикулярных импульса движения этого тела в пространстве и импульса движения его во времени , который мы называли еще "импульсом покоя" тела.

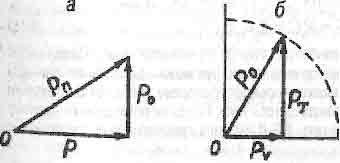Рис. (5.3)

А почленно домножив (5.9) на С2(с квадрат), получили известное в СТО, но бывшее до сих пор для многих загадочным уравнение (2.12), связывающее полную энергию тела с импульсом Р.

(5.10)

Треугольник импульсов на рис. 5.3а объясняет, почему в этом уравнении энергии и импульс связаны так странно. До появления теории движения СТО не могла дать такого простого объяснения.
Попробуем теперь почленно домножить основное уравнение (1.16) на . Получим еще одно уравнение для импульсов:

(5.11)

в справедливости которого нет оснований сомневаться. Оно описывает еще один треугольник импульсов, изображенный на рис. 5.36. В нем

- (5.12)

это классический импульс движения в пространстве со скоростью V тела, обладающего массой покоя m0. Таковым считали импульс тела до появления теории относительности. А импульс

(5.13)

это аналогичный по форме предыдущему "классический" импульс движения того же тела во времени.
В треугольнике на рис. 5.36 "импульс покоя" Р0 является гипотенузой, то есть суммарным вектором, складывающимся из взаимно перпендикулярных импульсов Рv и Рт. При движении тела величины Pv и Рт взаимосогласованно изменяются с изменением скорости движения так, чтобы величина Р0 осталась неизменной (инвариантной).
Если почленно домножить уравнение (5.11) на С2 (с квадрат), получим:

(5.14)

Мы специально перенесли здесь член в правую часть, чтобы придать нашему уравнению (5.14) такую же структуру, как у известного уравнения (5.10).
Нетрудно увидеть, что наше уравнение (5.14) определяет суммарную энергию ЕЕ вращающегося тела, о которой мы говорили в разделе 4.4, так как

(5.15)

Существенным отличием уравнения (5.14) от (5.10) является наличие знака минус вместо плюса между слагаемыми правой части. Тут можно было бы по примеру создателей СТО начать придумывать "псевдопифагорову теорему" о сложении компонент энергий-импульсов вращающегося тела. Но мы не последуем их дурному примеру, так как перед нами на рис. 5.3 б имеется прямоугольный треугольник, который всё объясняет.
Попытаемся записать уравнения (5.14) и (5.10) одной общей формулой:

(5.16)

В случае поступательного движения тут P = mV - реальный импульс движения тела в пространстве, а в случае вращательного - мнимый импульс

(5.17)

Будучи в формуле (5.16) возведенным в квадрат, он дает знак минуса, который мы видели в (5.14).
Казалось бы, что здесь мы условно и чисто формально назвали импульс Pv, относящийся к вращательному движению, мнимым только для того, чтобы получить знак минуса в нужной формуле. Но удивительно, как всё сходится с тем, что мы уже говорили ранее о мнимости скорости вращательного движения!
Да, природу не обманешь и не запутаешь. Треугольник на рис. 5.36 настойчиво показывает, что один из взаимно перпендикулярных импульсов (Рт или Pv) мы должны называть мнимым.
А из уравнений (5.14) и (5.15) хочешь, не хочешь, а надо признать, что действительным следует считать импульс Рт, так как наблюдаемой (реальной) при вращении тела является суммарная энергияСледовательно, перпендикулярный ему импульс Pv мы вынуждены считать мнимым. Это хорошо согласуется с выводами раздела 1.5, в котором было показано, что в "вертикальном запредельном мире мальтийского икса - действительная величина, a ßr-мнимая.

5.3. Загадочные торсионные поля

В разделе 1.2 мы обращали внимание на то, что в выражении для квадрата комплексной длины (1.7) мнимая часть 2Cdtdl ускользнула от внимания разработчиков СТО. Но в ОТО она была неявно учтена и в конечном счете легла в основу представления о кривизне пространства-времени. Эйнштейн еще в 1916 г. связал гравитацию с кривизной пространства-времени.
А в начале 20-х годов французский математик Э. Картан предположил, что может существовать взаимосвязь некоторых физических величин и с другим геометрическим понятием - кручением [43]. Если кривизна характеризует степень отклонения линии от прямолинейности, то кручение характеризует степень отклонения линии от плоской формы.
В рассмотренной нами в разделе 4.3 модели движение в пространстве-времени сводилось к движению материи частицы по винтовой линии. Если эта модель верна, то всякое движение должно сопровождаться кручением.
Кручение винтовой линии математики выражают формулой [44]:

(5.18)

в которой R- радиус винтовой линии, b - ее шаг. Кручение правой винтовой линии принято считать положительным, левой - отрицательным.
Картан разрабатывал теорию гравитации с кручением, но на его работы тогда не обратили внимания, поскольку в то время еще не был открыт спин элементарных частиц, тесно связанный с кручением. Тем не менее Э. Картан первый указал на возможность существования полей, порождаемых угловым моментом вращения тел позднее (в 70-е годы) названных торсионными полями (от фр. торсион - кручение.)
Лишь в 60-е годы кручение было окончательно введено в уже достаточно разработанную к тому времени теорию гравитации Эйнштейна. Например, в работах польских физиков А. Траутмана [45] и В. Копчинского [46] было показано, что кручение пространства-времени может устранять космологическую сингулярность в нестационарной модели Вселенной.
Академик РАЕН А.Е. Акимов, возглавивший в 90-е годы исследования по торсионным полям в Международном институте теоретической и прикладной физики (г. Москва), рассказывал, что на мысль о необходимости существования полей вращения его навели рассуждения старейшего японо-американского физика-теоретика Утиямы. Последний утверждал, что полей в природе должно быть столько, сколько у элементарных частиц имеется независимых свойств. Так, электрическим зарядам соответствует электромагнитное поле, массе - гравитационное. Продолжая эту цепочку, можно предположить, что спину - квантовому аналогу углового момента вращения - должно соответствовать поле вращения, которое может действовать только на частицы, обладающие спином. (Подобно тому, как электрическое поле действует только на частицы, обладающие зарядом.)
Возможно, что дорога к пониманию роли кручения была бы короче, если бы разработчики СТО с самого начала пошли по пути теории движения, предложенному, увы, лишь в [8]. В этой теории квадрат комплексной скорости движения* (* Как мы уже указывали, лишь квадраты динамических характеристик играют роль в СТО.)описывается выражением

(5.19)

Если почленно домножить это выражение на "импульс покоя" ш0С, то мнимая часть будет выражать не что иное, как удвоенное количество вращательного движения, на что указывалось в [9], где делается вывод, что всякое движение должно сопровождаться вращением, и что вращение является неотъемлемым свойством материи.
И действительно, в природе все тела вращаются или обращаются, начиная от элементарных частиц и кончая..., нет, не галактиками, которые, как известно, вращаются, а всей Вселенной, которая, оказывается, тоже вращается [47, 48].
Мы не первые пришли к такому выводу. Выпускник МГУ Г.И. Шипов в 60-е годы, в отличие от нас, не сомневался в правильности теории Эйнштейна. Ознакомившись с его программой создания единой теории поля, он пишет работу [49] о геометризованном варианте электродинамики, в которой в качестве системы отсчета использует не только инерциальные, но и ускоренные локально лоренцевы системы, связанные с зарядом. В получившейся "общерелятивистсткой электродинамике" появляются необычные свойства: во-первых, допускается ускоренное безызлучательное движение зарядов в поле центральных сил (что объясняло первый постулат Бора), во-вторых, энергия электрического поля точечного заряда оказывалась конечной величиной (в результате устранялись известные расходимости электродинамики).
Продолжая работу в том же направлении в 70-е годы, Шипов переходит от геометрии Римана, которой пользовался Эйнштейн, к геометрии Римана-Картана, описывающей не только риманову кривизну, но и кручение. Уравнения геодезических пространств Римана-Картана после умножения на пробную массу содержали дополнительную силу, рождаемую кручением. Когда эта сила равна нулю, получались обычные уравнения движения теории гравитации Эйнштейна. Когда же дополнительная сила была ненулевой, появлялось излучение заряда.
Шипов догадывался, что источником римановой кривизны пространства может являться его кручение. Если бы это оказалось действительно так, то это означало бы, что кручение пространства лежит в основе всех полей и частиц и является первопричиной всего в природе. И в случае доказательства это был бы большой шаг к созданию единой теории поля.
Но Шилову не нравилось, что тензор кручения в геометрии Римана-Картана не носит потенциального характера, то есть не может быть представлен в виде производных от геометрических величин. (А автор вслед за Эйнштейном стремился к геометризации физики.) Кроме этого, Шипов подметил, что кручение определяет кривизну пространства только тогда, когда полный тензор кривизны в геометрии Римана-Картана равен нулю. Последнее означало, что для построения теории, в которой кручение является причиной римановой кривизны (а значит и полей), пригодна только геометрия абсолютного параллелизма. (По определению, пространство обладает абсолютным параллелизмом, если его тензор кривизны
обращается в нуль.)
Тут мы должны отметить, что у пространства, описываемого эвклидовой геометрией, кривизна всегда равна нулю. (Такое пространство еще называют плоским.) Это говорит о том, что Шипов в конце-концов неосознанно пришел к тем же выводам о необходимости признания пространства нашей Вселенной плоским, к каким мы пришли в разделе 1.4.
Шипов отмечает, что "замечательным свойством геометрии абсолютного параллелизма является то, что ее кручениеимеет потенциал, в качестве которого выступает тетраэда :

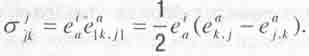(5.20)

В 1976 г. он публикует работу [50], в которой показывает, что если в качестве пространства событий использовать пространство не с геометрией Римана, а с геометрией абсолютного параллелизма, то легко решается проблема геометризации правой части тензорного уравнения Эйнштейна для поля тяготения:

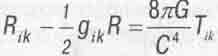(5.21)

Сам Эйнштейн, как известно [51], сравнивал это уравнение с дворцом одно (левое) крыло которого (описывающее геометрию пространства-времени) выстроено из ^красного мрамора, а другое (правое) - описывающее вещество и поля - сделано плохого дерева. Ибо тензор энергии-импульса материи Тik в правую часть этого Уравнения Эйнштейн ввел фактически искусственно, феноменологически, без должного обоснования. Он считал такое положение временным и много сил затратил на то, чтобы найти уравнения поля с геометризованной правой частью. Геометризация полей, определяющих тензор энергии-импульса материи, и являлась частью эйнштейновской программы создания единой теории поля. Кроме того, Эйнштейн считал, что геометризация полей материи позволит найти уравнения "совершенной квантовой теории" [52].
Новое уравнение поля Шилова-Эйнштейна было записано в виде:

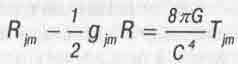(5.22)

где тензор энергии-импульса материи

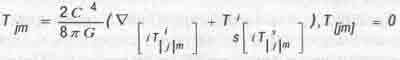(5.23)

уже имеет геометрическую природу (мечта Эйнштейна) и посредством "поля материи"

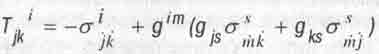(5.24)

определяется через кручение (5.20) геометрии абсолютного параллелизма.
В дальнейшем Шилову удается установить, что поля, образующие тензор материи Тjk' в полностью геометризованных уравнениях Шилова-Эйнштейна, оказываются полями инерции, выражающими силы инерции в ускоряемых системах отсчета [53]. Автор делает вывод, что источником полей инерции и причиной появления сил инерции является четырехмерное вращение системы отсчета. При этом прямолинейному ускоренному движению материальной точки в трехмерном пространстве соответствует, как известно из СТО, поворот (вращение) оси времени относительно начала координат в четырехмерном пространстве-времени. Этим была решена важнейшая задача механики о причинах сил инерции, будоражившая умы со времен Ньютона.
Отметим, что с учетом сказанного в разделе 2.5, решение Шилова проблемы сил инерции отдаленно перекликается с формально найденным в [8] решением той же задачи.
Заменив материю кручением пространства, Шипов пишет, что "в мире не происходит ничего, кроме изменений кривизны и кручения пространства". Он показывает, что четырехмерное вращение системы отсчета, вызываемое полями инерции ту, связано с кручением пространства событий в его всеобщей теории относительности:

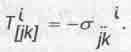(5.25)

Поля, определяемые кручением, к тому времени уже получили название торсионных полей. И если верить Шилову, то поле инерции Тjk' представляет собой торсионное поле, порождаемое кручением пространства абсолютного параллелизма.
В первоначальной теории Эйнштейна-Картана полагали, что кручение пространства-времени, в отличие от других физических полей, не может распространяться в пространстве, поскольку константа возникающих взаимодействий, принимавшаяся в этой теории равной произведению гравитационной постоянной G на постоянную Планка Л, оказывалась на 27 порядков величины меньше константы гравитационных взаимодействий, составляющей ~10-38(10 в минус 38 степени). Из этого следовало, что если эффекты кручения и существуют, то они настолько слабы, что практически ненаблюдаемы.
Но ряд экспериментальных работ, обзор которых дан, например, в [54], заставил некоторых теоретиков в 70-е годы пересмотреть представление о константе спин-торсионных взаимодействий и предположить, что она больше константы гравитационных взаимодействий и составляет ~10-5(10 в минус 5 степени) -10-6(10 в минус 6 степени). Такая величина константы принималась и в теории электроторсионных взаимодействий Г.И. Шилова [55].
Экспериментами, стимулировавшими данные работы теоретиков, были сначала проведенные в 1972 г. опыты Ч. Эмбера [56], показавшие, что поляризованная по кругу электромагнитная волна испытывает снос из плоскости падения так, что направление сноса определяется знаком кручения волны. А затем в 1977 г. был эксперимент А. Тама и В. Хаппера [57], показавший, что циркулярно поляризованные лучи лазеров в спинирующеи среде взаимно притягиваются или отталкиваются в зависимости от соотношения знаков их кручений (поляризации). На наличие торсионных эффектов указывал и ряд сообщений о необычном поведении гироскопов (изменение их веса в зависимости от скорости и направления вращения и др.) [34, 58-62].
Теория торсионных полей, развитая Шиповым, Акимовым и другими, далеко еще не закончена и во многом эвристическая. А потому она представляется некоторым скептикам "высосанной из пальца". Она предполагает, что наличие торсионных полей обуславливается только вращением тел и частиц и не зависит от их заряда, точно так же, как электромагнитное поле зависит только от заряда тела и не зависит от его массы. При этом торсионное поле может порождаться как внутренним вращением элементарной частицы - ее спином, так и макроскопическим вращением тел [63].
Г. И. Шипов в [55] утверждает, что первичными торсионными полями являются вакуумные возбуждения без массы и заряда, обладающие трехмерным спином. Он пишет, что пространство в области, занятой вакуумным возбуждением, вращается, но тензор энергии-импульса первичных торсионных полей равен нулю. А это означает отсутствие переноса энергии при их распространении.
Поскольку первичные торсионные поля при своем распространении не могут передавать веществу импульс и энергию (из-за отсутствия у них таковых), то это должно обеспечивать их огромную проникающую способность при прохождении через вещество. Тем не менее, утверждают создатели теории торсионных полей, последние, не перенося энергию, все же способны к взаимодействию с веществом. Например, способны поворачивать плоскость поляризации света, фактически не затрачивая на это энергии. Отсюда делается вывод, что торсионные поля способны передавать информацию на расстояние без передачи энергии. Поэтому разработчики торсионных полей еще называют их информационными полями и даже "пси-полями" (от слова психо), связывая с этими полями наличие разума у живых существ [63, 64].
Рассматривая нейтрон как систему из протона и электрона, находящегося в потенциальной яме торсионного поля, создаваемого этой системой, Шипов в [55] приходит к выводу, что рождение нейтрино при распаде нейтрона представляет собой излучение безмассового торсионного поля при выходе электрона из торсионной потенциальной ямы. Таким образом, нейтрино по Шипову представляет собой "разновидность материального торсионного поля, уже переносящего энергию". Высокую проникающую способность нейтрино Шипов объясняет чрезвычайно слабым взаимодействием торсионных полей с веществом.
К этому мы добавим, что вторичное квантование торсионного поля, осуществленное по аналогии с вторичным квантованием электромагнитного и гравитационного полей, будь оно сделано, определило бы квант торсионного поля и таким образом выявило бы переносчика торсионных взаимодействий. Поскольку вторичное квантование -задача математически чрезвычайно сложная и никем для торсионных полей пока не осуществленная, отметим только, что и без ее решения интуитивно понятно, что переносчиком торсионных взаимодействий являются, по-видимому, нейтрино. Действительно, нейтрино - единственная элементарная частица, обладающая только одним квантовым числом - спином и спиральностью. Поэтому нейтрино почти идеально подходят на роль переносчиков кручения, характеризующего торсионные поля. Мы говорим "почти" потому, что нейтрино, помимо спина, несут с собой еще и энергию, и импульс, что как-то не вяжется с шиповским представлением о торсионных полях.
Все станет на свои места и противоречия устранятся, если мы вспомним, что при анализе теории тахионов с позиций теории движения в книге [9] был сделан вывод, что нейтрино могут являться тахионами, то есть двигаться со сверхсветовыми скоростями. Если это действительно так, то скорости нейтрино должны быть тем выше, чем меньше их энергии. Только у высокоэнергетичных нейтрино (несущих энергию > 1 кэВ) скорость снижается почти до скорости света в вакууме С. С этой точки зрения переносчиками первичных торсионных полей Шипова, имеющих нулевой тензор энергии-импульса, можно считать трансцедентные тахионы-нейтрино, имеющие бесконечно большую скорость, но не несущие энергию [9].
Шипов и Акимов тоже догадались, что переносчиками торсионных взаимодействий должны являться нейтрино. Но эти авторы никогда не считали нейтрино тахионами, а потому не вели речь о трансцедентных нейтрино, а писали, что "в качестве квантов торсионного поля выступают низкоэнергетические реликтовые нейтрино" [65]. За это они подверглись уничижительной критике в [66], где вскрываются некоторые возникающие в связи с этим противоречия. Одно из них - то, что скорость реликтовых космологических нейтрино считается равной скорости света С, а теория Шипова требовала мгновенного распространения торсионных полей.
Из этой теории следовало, что скорость распространения торсионных полей по крайней мере на 9 порядков величины больше скорости света в вакууме С. Шипов и Акимов говорят, что первым экспериментальным подтверждением этого для них явились результаты известных астрономических наблюдений знаменитого пулковского астронома Н. А. Козырева, доложенные в 1976 г. на симпозиуме в Бюракане [67].
Козырев наблюдал звезды в телескоп-рефлектор, закрытый непроницаемой для электромагнитных волн крышкой. И обнаружил, что когда телескоп направлен в некоторые участки неба, сопротивление чувствительного к теплу резистора, помещенного в фокальной плоскости, изменяется. Такие сигналы регистрировались при трех направлениях телескопа. Первое - когда направление соответствует оптическому изображению объекта (звезды или галактики). При этом сигнал идет вместе со светом "из прошлого", так как приходящий свет от звезды был излучен ею много лет назад и все эти годы находился в пути к нам. Второе - когда направление соответствовало "истинному" (расчетному) положению объекта в момент наблюдения. (Мгновенно приходящий сигнал из "настоящего"). Третье направление соответствовало положению объекта в тот момент времени, когда свет, излученный в точке наблюдения (с Земли), долетит до этого объекта (сигнал "из будущего").
Это сообщение пулковского астронома тогда было встречено со скептицизмом, и более 10 лет почти никто не воспринимал его всерьез, настолько оно казалось неправдоподобным. Лишь в 1990 г. группа астрономов, возглавляемая академиком M. M. Лаврентьевым [68], и независимо от них киевский астроном А. Ф. Пугач [69] повторили и подтвердили наблюдения по методике Козырева.
Сторонники теории торсионных полей интерпретировали эти результаты как наблюдения передачи сигналов посредством торсионных полей, излучаемых вращающимися звездами и галактиками. При этом объясняли, что торсионное излучение имеет запаздывающую и опережающую составляющие, точно так, как в радиофизике электромагнитную волну рассматривают как суперпозицию запаздывающей и опережающей волн.
В теории электромагнитных волн опережающую компоненту, движущуюся к излучателю со всех сторон небосвода (словно она была излучена множеством таких же излучателей, удаленных на бесконечность), считают чисто теоретическим казусом, за которым кроется лишь какой-то недостаток теории, а не физическая реальность [17]. А вот теория движения, изложенная в [9], может дать физическую трактовку опережающей компоненты как в торсионных полях, так и в электромагнитных волнах.
Опережающая компонента движется из будущего в прошлое и суммируется в настоящем с запаздывающей компонентой, движущейся из прошлого в будущее. Но чтобы очутиться в будущем, поле, создающее там опережающую компоненту волны, должно было сначала улететь от своего источника в это будущее, улететь со скоростью движения во времени у, намного опережающей нормальную скорость движения во времени запаздывающей компоненты. Это возможно только когда y ~ 1. А в [9] было показано, что значений y>1 могут достигать как тахионы, так и быстро вращающиеся тела. Это значит, что переносчики торсионных взаимодействий - низкоэнергетичные "вращающиеся" (обладающие спином) нейтрино - могут улететь от нас в будущее, а став там трансцедентными, поворачивать вспять как в своем движении в пространстве, так и в движении во времени. В теории тахионов это называется инверсией [15]. Как юказано в [9], трансцедентными низкоэнергетичные тахионы становятся при этом в потому, что на пути в бесконечность что-то отняло у них последнюю энергию, а потому, что за время их полета источник (например нуклон), совершающий квантовые .нулевые) колебания, называемые циттербевегунгом, изменил направление этого микродвижения на противоположное, в результате чего скорость относительного движения тахиона относительно источника становится критической. Повернувшие вспять тахионы и образуют ту самую "рожденную на бесконечности" опережающую компоненту волны, которая вот уже более ста лет оставалась в электродинамике загадкой за семью печатями.
Улавливание сигналов, передаваемых с помощью торсионных полей, которые, по уверениям А. Е. Акимова, в Международном институте теоретической и прикладной физики РАЕН научились не только излучать, но и уверенно принимать, осуществляют за счет того, что "безэнергетичные", как о них думают, торсионные поля все же каким-то образом влияют на физические процессы, происходящие в атомах и молекулах вещества, а уже эти процессы сопровождаются выделением или поглощением энергии
[70].
Шипов и Акимов утверждают, что торсионное поле изменяет ориентацию спинов электронов в облучаемом торсионным излучением материале, а уже это изменение вызывает лавинообразное протекание тех или других процессов в данном материале или системе, если она находилась в состоянии неустойчивого равновесия и необходим был лишь малейший толчок для выхода из этого состояния. Поэтому Шипов сравнивает торсионный сигнал со спусковым крючком, управляющим мощным выстрелом.
Разработав теорию торсионных полей, Г. И. Шипов попытался в [55] объяснить с помощью этой теории все многообразие окружающей нас природы, и в первую очередь сущность физического вакуума, полей, материи и вещества.
С позиций теории движения нам теперь понятно, что поскольку Шипов подходил к построениям Эйнштейна не критически, например так же ошибочно трактовал интервал, как расстояние между точками пространства-времени, то, по-видимому, не всё в его теории торсионных полей может оказаться правильным, Но думается, что основное в общих чертах он все-таки выявил, хотя многое из найденного им можно было бы вывести проще, вооружившись теорией движения. В этом мы убедимся в следующем разделе.

5.4. Волны де Бройля и торсионные поля

Мы уже упоминали в разделе 4.3, что Луи де Бройль в 1924 г. ввел понятие "волн материи", групповая скорость которых Vгр совпадает со скоростью движения частицы в пространстве, а фазовая . Для движущихся частиц, масса покоя которых не равна нулю, Vф может быть только больше скорости света. Но насколько материальны "волны материи"? И что за волновой процесс они описывают?
Э. Шредингер высказал в свое время предположение о том, что волновой пакет этих волн, локализованный в малой области пространства, представляет элементарную частицу. Но наличие дисперсии, то есть зависимости фазовой скорости волн де Бройля от их частоты даже в вакууме, должно было приводить к тому, что волновые пакеты, состоящие из таких волн, расплываются со временем. А элементарные частицы стабильны.
Большинство теоретиков до сих пор полагают, что фазовая скорость волн де Бройля имеет чисто символическое значение и не отражает никаких конкретных процессов. Но некоторые физики называют волну де Бройля "волной-пилотом", которая опережает движение частицы и как бы разведывает ей путь. В результате частица "знает" через какое из двух отверстий перегородки, установленной на ее пути, ей проскочить, а после проскоков через эти отверстия многих следующих друг за другом частиц на экране за перегородкой получают интерференционную картину, обусловленную интерференцией "волн-пилотов", проходивших одновременно через оба отверстия, хотя каждая из частиц пролетала только через одно из них, а каждая последующая частица начинала движение только после того, как предыдущая уже закончила свой путь [71]. Получается, что не такой уж нереальной оказывается сверхсветовая фазовая скорость волн де Бройля. Ведь частицы в этих экспериментах летели почти со световой скоростью, а волна де Бройля намного опережала их. Плоская бегущая волна де Боойля намного опережала их.
Плоская бегущая волна де Бройля

(5.26)

описывает, как известно [72], свободное движение материальной частицы. Здесь - некая функция, характеризующая вероятность нахождения частицы в данной точке пространства в данный момент времени, как об этом догадался в 1927г. М.Борн.
r - радиус-вектор положения точки в пространстве,
k - волновой вектор, связанный с импульсом частицы соотношением

(5.27)

со - циклическая частота волны, определяемая формулой Планка E = h, в которой Е- энергия частицы.
Разлагая экспоненциальный сомножитель в (5.26) по формуле Эйлера для комплексных чисел и пренебрегая мнимой частью разложения, как пренебрегают ею и при рассмотрении аналогичных уравнений для электромагнитных волн [73], получают:

(5.28)

Косинус здесь можно раскрыть в виде:

а скалярное произведение векторов - в виде:

(5.29)

где - угол между векторами
При совмещении начала координат с центром, вокруг которого обращается с циклической частотой Ω частица, скалярное произведение (5.29) для всех точек, лежащих на круговой орбите, по которой обращается частица, в моменты нахождения в этих точках частицы оказывается равным нулю (так как cos 90° = 0). Тогда выражение (5.28) упрощается в этих точках до .
Если понимать - функцию как величину, характеризующую вероятность нахождения частицы в данной точке пространства-времени, то последнее выражение говорит, что эта вероятность максимальна в данных точках орбиты. Но она максимальна тут лишь в моменты, когда cos. В остальные моменты времени здесь и надо говорить о суперпозиции двух гармонических процессов с частотами .
Когда эти частоты близки, но не равны друг другу, должны наблюдаться биения, а когда отношение / оказывается целым числом, то возникает стоячая волна. Таковая наблюдается, например, при обращении электрона по стационарной орбите вокруг ядра в модели атома Бора.
До сих пор мы в данном разделе излагали давно известные азы квантовой механики. А теперь обратим внимание на то, что вдоль направления оси вращения cos в любые моменты времени t, a потому здесь

(5.30)

в любые моменты времени.
Понятно, что на оси вращения так определенная - функция описывает уже отнюдь не вероятность нахождения частицы, а нечто иное, ибо частица, летящая по орбите вокруг оси вращения, никак не может оказаться на этой оси. Но на этой оси находится центр масс вращающейся системы. Значит, когда формула (5.30) указывает, что на оси вращения вероятность нахождения чего-то максимальна, то, оказывается, формулы не лгут! Но удивительно, что тут центр масс описывается как материальная точка, даже если в этом центре нет никакого материального тела, как в случае двойной звезды или позитрония.
А вот в сколь угодно близких к оси вращения ее окрестностях функция ( r t) уже является периодической (гармонической) функцией от расстояния г до центра вращения, - функция здесь попеременно принимает то положительные, то отрицательные значения, так как cos здесь изменяется с ростом r периодически в пределах от +А до -А, где А - малое число, меньшее единицы. А это значит, что при вращении аксиально симметричного тела вокруг его оси симметрии - - функции, задаваемые диаметрально противоположными частями тела, суммируясь здесь с противоположными знаками, будут давать в результате нуль.
Возможно ли, чтобы вдоль оси вращения вероятность нахождения здесь центра масс вращающейся системы тел была равна единице, а в сколь угодно близкой к ней окрестности становилась нулевой? Общие принципы квантовой механики указывают, что нет, вероятность должна спадать постепенно по мере удаления от оси вращения. Значит, где-то в наши выкладки вкралась ошибка.
И вот тут-то нам поможет теория движения. Из нее следует, как было убедительно показано в разделах 5.1 и 5.2, что вращательное движение - это мнимое движение, и тангенциальная скорость Vr как и импульс вращательного движения Рr должны описываться мнимыми числами. Тогда, в соответствии с (5.27), и волновой вектор k частицы, движущейся по круговой орбите, должен быть мнимым.
А если так, то при круговом движении частицы мы вместо (5.28) получаем несколько другую формулу для волн де Бройля:

(5.31)

Эта формула опять описывает стоячую волну, но отличается наличием сомножителя обуславливающего экспоненциальное затухание волны с увеличением расстояния r от центра вращения. При этом затухание в разных направлениях происходит по-разному. В плоскости орбиты оно минимально вдоль направления от
центра вращения к частице (при таком направлении векторы взаимно перпендикулярны), и формула (5.31) здесь превращается в (5.30).
И вдоль оси вращения функция (r,t) по-прежнему описывается формулой (5.30) и не затухает с расстоянием r. В этом все пока совпадает с выводами, полученными из общепринятой квантовой теории.
Различие же проявляется уже в ближайшей окрестности от оси вращения. Здесь cos (kr sin t) по-прежнему изменяется в пределах от +А до -А, но теперь этот косинус является уже не сомножителем произведения, а стоит в показателе степени экспоненциального сомножителя выражения (5.31). Потому где В -число, много меньшее единицы. Это означает, что теперь - функции, задаваемые диаметрально противоположными частями вращающегося аксиально симметричного тела, в близких к оси вращения ее окрестностях уже не будут знакопеременными величинами, и их суммирование даст не нуль, а конечную величину. То есть вероятность нахождения здесь центра масс тела будет не нулевой, а хоть и очень малой, но конечной величиной.
Так с помощью теории движения мы достигаем естественного плавного и непрерывного распределения -функции в пространстве возле оси вращения. Это еще раз показывает, что теория движения с ее представлением о вращательном движении как мнимом верна.
Вернемся к тому обстоятельству, что формула (5.31) описывает стоячую волну. Стоячая волна, как известно, предполагает отсутствие перетекания энергии через ее узловые точки. Но в промежутках между узловыми точками (в пучностях волны) происходит какое-то движение, превращение одного вида энергии в другой и обратно по гармоническому закону. Какое движение описывает формула (5.31 ) вне точек орбиты частицы? Колебательное движение квантовых осцилляторов физического вакуума? Или виртуальных частиц какого-то поля? Но ясно, что формула (5.31) описывает какое-то поле.
Поскольку в этой формуле фигурирует греческая буква , можно назвать это поле "пси-полем вращения". И получаем удивительное совпадение: пси-полем И. Шипов и А. Е. Акимов в своих публикациях иногда называют торсионное поле! Только у них приставка "пси" произошла от слова "психофизика", основы которой
они усматривают в торсионных полях.
Если наше выражение (5.31) описывает стоячую, а не бегущую волну, которую описывала формула де Бройля (5.26), то это означает, что пси-поле, описываемое нашей формулой (5.31), не распространяется в пространстве от точки к точке, а возникает во всех его точках, можно сказать, мгновенно в момент появления источника
токого поля. Это опять же совпадает с выводами Шилова и Акимова о торсионных полях. А мгновенность распространения поля предполагает, в соответствии с теорией тахионов [15] и рассмотрения тахионов с позиций теории движения в [9], отсутствие переноса таким полем энергии. И это тоже соответствует выводам Шилова о свойствах торсионных полей.
Кроме вышесказанного, из выкладок данного раздела, пожалуй, ничего нельзя сказать большего о скорости распространения торсионных полей, с которыми мы вынуждены отождествить так определенное нами -поле. Мы здесь даже не пытались составить для него волновое уравнение, в которое входила бы скорость распространения волн. Но отметим, что аналогом классического волнового уравнения Даламбера в квантовой механике для волн де Бройля является уравнение Шредингера, решением которого и служат уравнения плоской волны де Бройля (5.26). И давно подмечено, что уравнение Шредингера дает точные решения лишь в предположении мгновенности распространения описываемых им "волн вероятности" [74].
Чтобы теория окупала хотя бы стоимость той бумаги, на которой написана, она должна позволять легко рассчитывать что-то конкретное. Для этого преобразуем формулу (5.31) в вид, более пригодный для практических вычислений. Вспомнив, что перепишем выражение (5.31 ) в виде:

(5.32)

Теперь здесь фигурируют не какие-то малопонятные величины и , а вполне привычные для инженеров, легко осознаваемые и измеряемые ими энергия E и импульс P частицы.
Подставив далее в полученное выражение (5.32) значения импульса и энергии E вращающейся системы из найденных выше формул (5.4) и (5.1), приведем выражение (5.32) к виду:

(5.33)

(Здесь)
При технических и даже космических скоростях Vr величина уr с большой точностью близка к единице. Это облегчает расчеты для тел, имеющих технические массы и скорости вращения. Для них экспоненциальный сомножитель в (5.33) оказывается исчезающе малым для всех точек пространства кроме точек орбиты тела и оси его вращения или обращения с ее близкими окрестностями, где этот сомножитель равен единице или близок к ней. Это означает остронаправленность возникающего - поля вращения (торсионного поля) вдоль оси вращения.
А вот для тел атомарных размеров ситуация существенно меняется. Например, для электрона, обращающегося в модели атома водорода со скоростью (где - постоянная тонкой структуры) вокруг ядра по первой боровской орбите, имеющей радиус , экспоненциальный сомножитель в (5.33) составит:

(Мы учли, что - это комптоновская длина волны электрона, равная .)
Значит, в пределах размеров атомов -поля вращения во всех точках атома достаточно велики.
Но для нас важнее уяснить, что они столь же велики вдоль всей уходящей в бесконечность оси вращения и атома, и его ядра, как вдоль оси вращения (спина) любой элементарной частицы.
Для лучшего понимания того, что рассматриваемые поля являются полями вращения или торсионными полями, учтем, что если произведение , фигурирующее в показателе экспоненты в (5.33), домножить на вектор радиус орбиты то получим выражение для момента количества движения M . Тогда

(5.34)

Теперь в полученном выражении показатель экспоненты равен отношению момента количества движения М данного тела к элементарному (минимально возможному в природе) моменту количества движения h, умноженному на отношение радиуса - вектора r данной точки пространства к радиусу вращения . Только теперь в показателе экспоненты фигурирует не скалярное, а векторное произведение .
В заключение этой главы отметим, что было бы очень любопытно и сравнительно несложно вычислить и градиент, и дивергенцию, и ротор от - функции, определяемой выражением (5.31 ), и тем самым найти систему уравнений, описывающих торсионное поле по аналогии с системой уравнений Максвелла, описывающих электромагнитное поле. Но такая задача выходит за рамки данной книги.

Выводы к главе

1. Тангенциальную скорость Vr вращательного движения тел и кинетическую энергию их
вращения следует считать мнимыми величинами.
2. При вращении тела скорость его движения во времени принимает значения, большие единицы. Эксперименты с ускорением мезонов в циклических ускорителях могут выявить это.
3. В отличие от импульса поступательного движения тела, в выражении для мнимого импульса вращательного движения Рг входит произведение скоростей движения тела в пространстве ßr и во времени уr а не их отношение.
4. График зависимости Pr отVr имеет экстремум-минимум при , а график зависимости кинетической энергии вращения тела от ут имеет минимум при .
5. Основное уравнение теории движения можно получить возведением в квадрат дифференциала комплексного числа , правильно описывающего точку в нашем пространстве - времени.
6. Полный импульс тела получается векторным сложением ортогональных импульса движения ) тела в пространстве P = mV и "импульса покоя" этого тела Р0= m0С. "Импульс покоя" тела Р0 получается векторным сложением ортогональных импульса движения тела во времени и классического импульса Pv= m0V.
7. Связь между полной энергией тела и импульсом тела P выражается известным уравнением котором Е0 - энергия покоя данного тела, а вот величина P = mV при поступательном движении тела в пространстве P = im0Vr - при вращательном движении тела, в чем состоит отличие от известного в СТО уравнения.
8.Из выражения для квадрата комплексной скорости в теории движения мнимую часть которого СТО упустила, следует, что всякое поступательное движение тела в пространстве должно сопровождаться вращением тела или кручением пространства, которое характеризует отклонение линии от плоской формы. Они описываются мнимой частью этого выражения. Вращение и кручение являются неотъемлемыми свойствами не только движения в пространстве, но и самого пространства-времени.
9. Всякое вращающееся тело порождает торсионные поля - поля кручения. Эти выводы хорошо согласуются с представлениями о торсионных полях, развитыми в работах Г. И. Шилова и А. Е. Акимова.
10. Переносчиками торсионных взаимодействий (квантами торсионного поля) являются, по-видимому, нейтрино, которые, согласно теории движения, являются тахионами и движутся со сверхсветовыми скоростями.
11. Представление о том, что вращательное движение мнимое, существенно изменяет выражение для плоских волн де Бройля, описывающих вероятность нахождения частицы в точках пространства при ее вращении или обращении по орбите. Теперь пси-функция оказывается стоячей волной, а вблизи от оси вращения вероятность нахождения частицы уже не нулевая, что обеспечивает необходимую плавность изменения - функции и разрешает ряд трудностей теорий де Бройля и Г. Шилова.
12. Пси-поле (торсионное поле), описываемое так модернизированными плоскими волнами де Бройля, имеет острую направленность вдоль оси вращения тела, генерирующего это поле, и возникает во всех точках пространства мгновенно, что означает бесконечно большую скорость распространения пси-волн торсионного поля.

Содержание